探讨二氧化硅纳米片、纳米管和纳米环的度量维数。

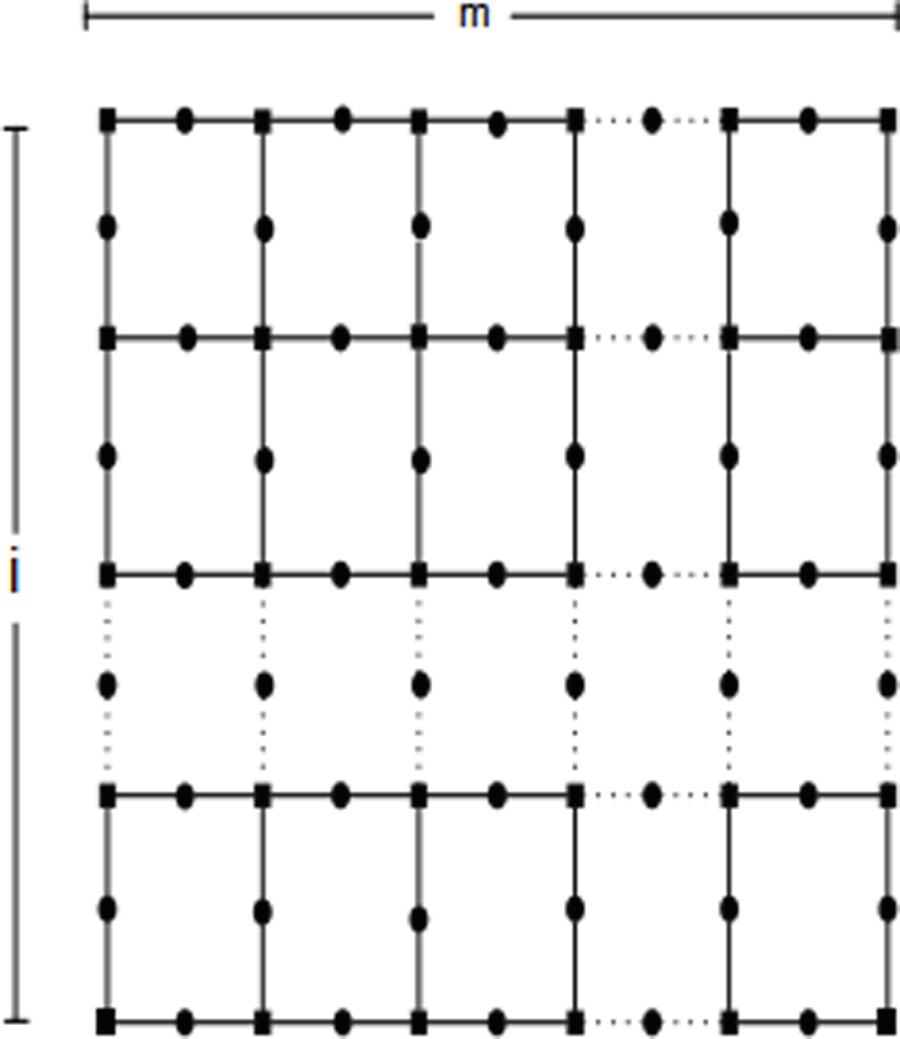
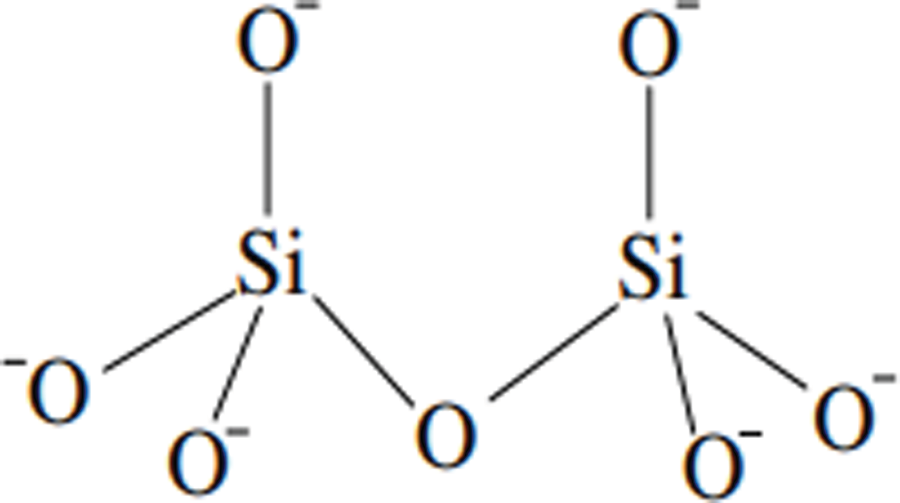
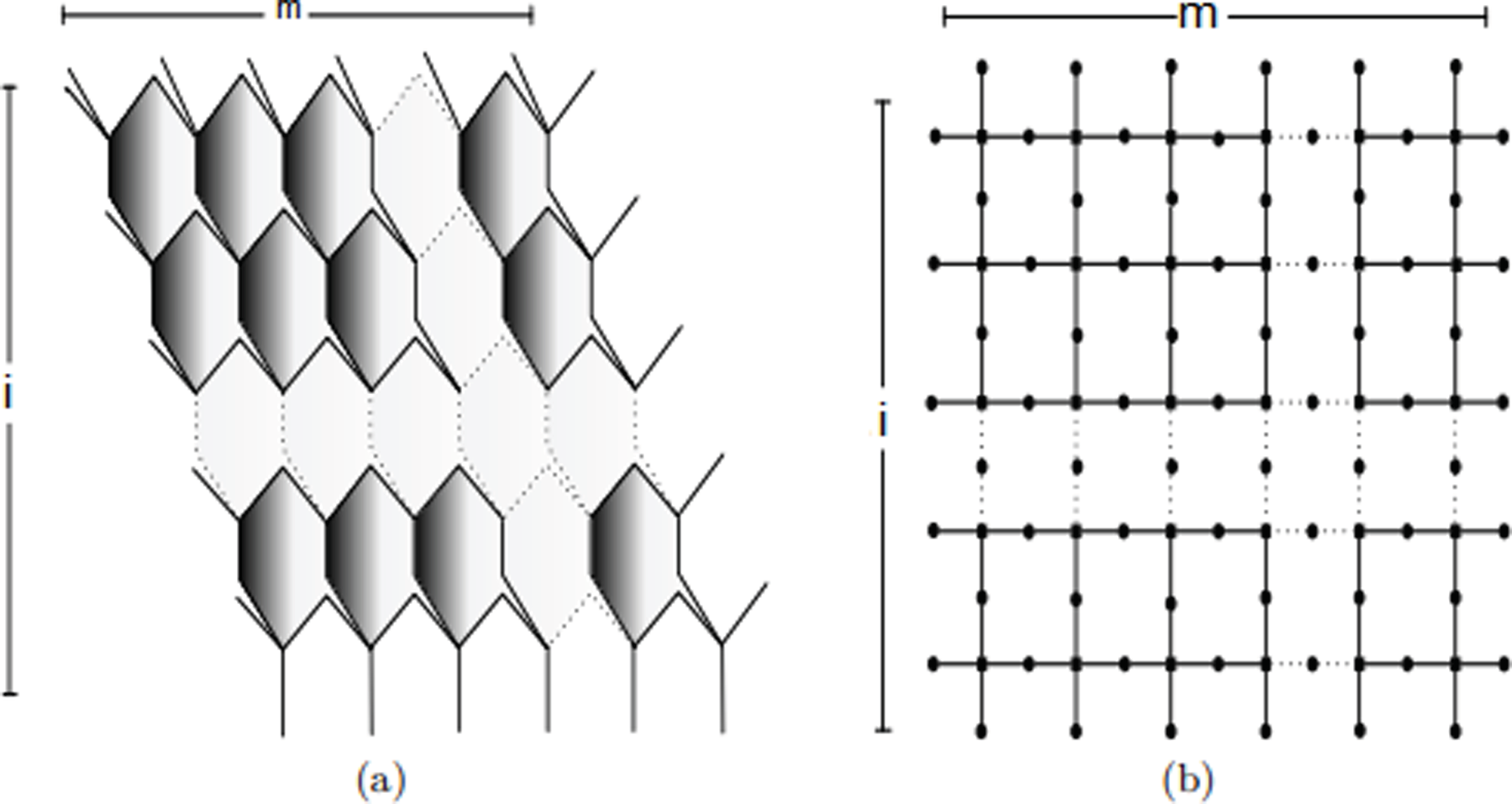
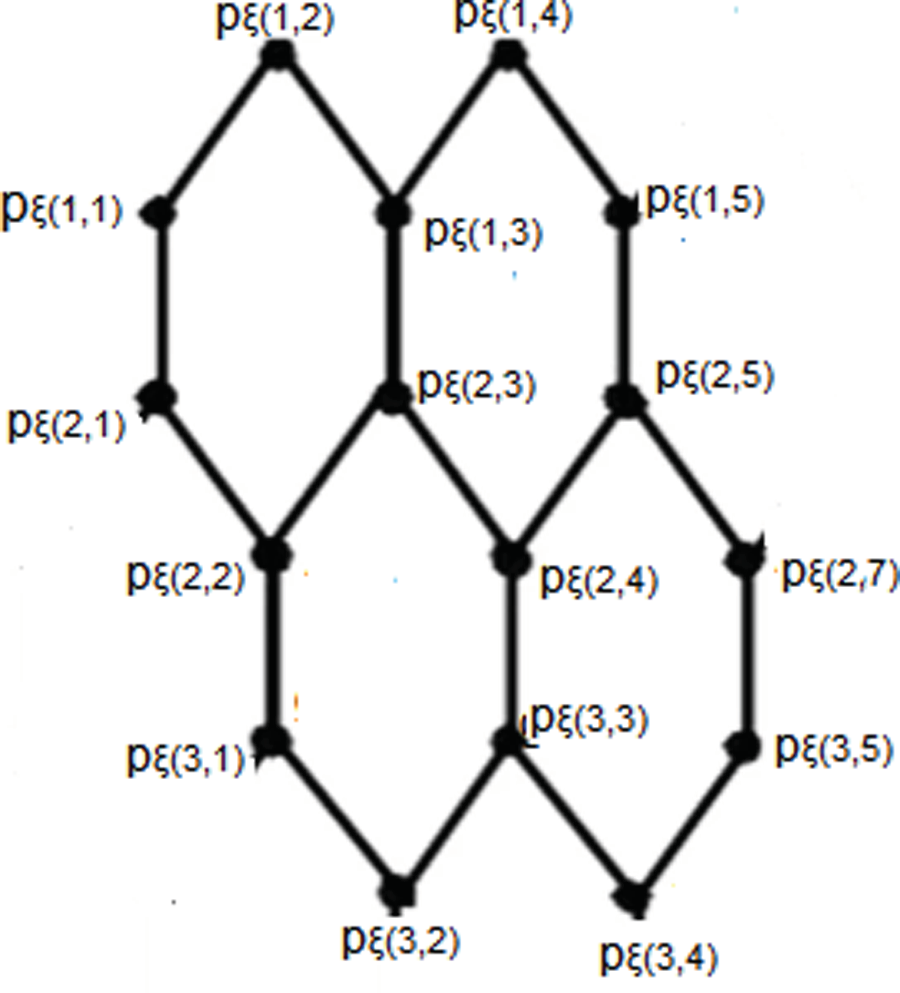
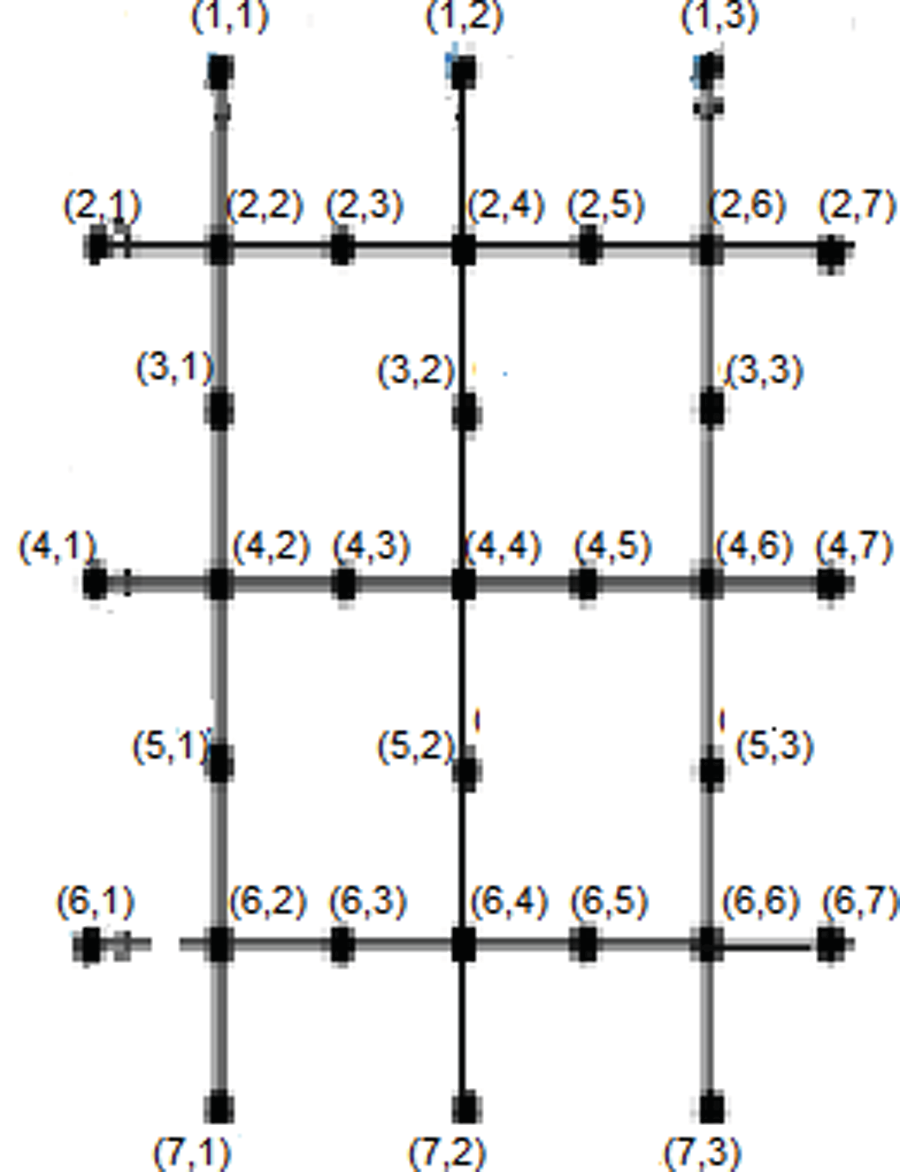
该文档主要探讨了二氧化硅（SiO2）纳米结构的度量维数（Metric Dimension, MD）和边度量维数（Edge Metric Dimension, EMD），特别是纳米片、纳米管和纳米环的结构。度量维数是图论中的一个概念，描述了在图中唯一识别每个点所需的最小顶点集，而边度量维数则是识别每条边所需的最小顶点集。理解这些维数对于表征纳米颗粒的几何和结构特性至关重要。

研究背景与动机

化学图论是图论的一个分支，主要用于通过图形化表示来研究化学结构。化学图论的目标是通过将化学结构表示为分子图（顶点代表原子，边代表原子间的键）来分析化学结构的物理性质。度量维数在化学科学中有广泛应用，因为它提供了一种定量方法来识别系统中的元素，从而解决工程、人工智能、计算、根管理、城市规划和建筑开发中的组织和优化问题。

研究方法

本文使用图论技术计算了各种SiO2纳米结构的MD和EMD，以阐明其独特的几何形状和配置。研究通过提供这些维数的精确公式，为设计和优化具有特定性质的SiO2基材料提供了重要的见解。研究中使用的图论方法包括度量基（metric basis）和解析集（resolving set）的概念，这些概念用于唯一识别图中的顶点或边。

研究发现

1. SiO2纳米片：由于其高表面积、稳定性和反应性，SiO2纳米片在催化、药物递送和电子设备中具有重要应用。其层状结构有助于功能团的附着，扩展了其在生化和电子领域的应用。

2. SiO2纳米管：这些结构提供了一个中空的核心，在药物递送和纳米流体学中具有优势，尤其是在需要控制释放和选择性吸附的领域。

3. SiO2纳米环：尽管研究较少，但SiO2纳米环在光学材料和光热药物递送中显示出潜力，得益于其独特的环状结构和可能的等离子共振。

研究贡献

本文首次系统地研究了SiO2纳米结构的MD和EMD，提供了这些结构的拓扑特征的详细描述。与之前仅计算拓扑指数的研究相比，本文提供的MD和EMD对于SiO2纳米结构的稳健表征至关重要。这些发现为化学、材料科学和纳米技术中的应用提供了宝贵的见解，特别是在纳米尺度上结构特征的理解方面。

结论

本文的研究为SiO2纳米结构的几何和结构特性提供了新的视角，强调了度量维数在表征和优化纳米材料中的重要性。通过详细分析SiO2纳米片、纳米管和纳米环的MD和EMD，研究为未来在化学、材料科学和纳米技术中的应用奠定了基础。

专业术语解释

• 度量维数（Metric Dimension, MD）：在图论中，度量维数是指能够唯一识别图中每个顶点的最小顶点集。
• 边度量维数（Edge Metric Dimension, EMD）：类似于度量维数，但用于识别图中的每条边。
• 化学图论：通过将化学结构表示为图（顶点代表原子，边代表原子间的键）来分析化学结构的物理性质的数学方法。

通过本文的研究，读者可以全面理解SiO2纳米结构的度量维数及其在纳米材料表征中的重要性，为进一步的研究和应用提供了坚实的理论基础。