量子时代数据安全保障的后量子密码学高级技术

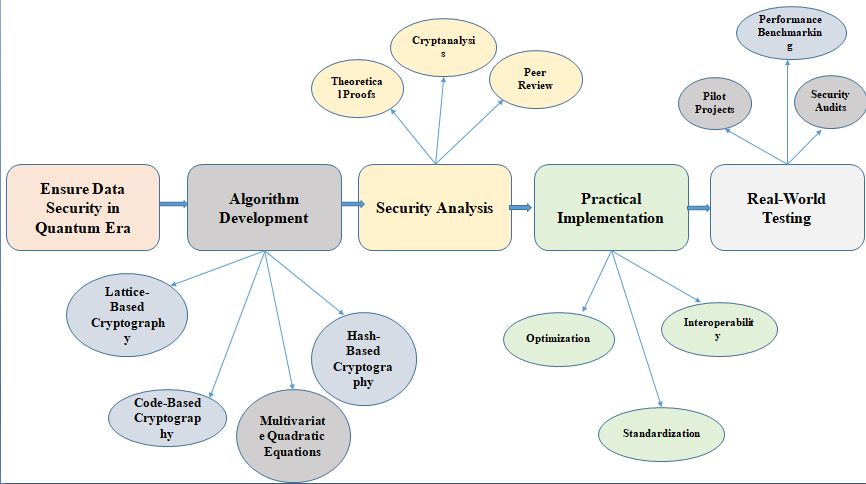
这篇论文探讨了后量子密码学（Post-Quantum Cryptography, PQC）的先进技术，以确保在量子时代的数据安全。随着量子计算机的出现，传统的安全方法面临重大威胁，因为这些方法依赖于离散对数和整数分解等难题的计算复杂性。本文旨在开发能够抵御量子攻击的安全策略。

引言部分指出，量子计算的到来将对当前的安全系统构成前所未有的挑战。许多流行的加密技术，如RSA和椭圆曲线密码学（ECC），都基于这些难题。然而，量子计算机可能使这些程序失效。

第二部分讨论了安全分析，即对后量子密码学方法安全性的研究。研究始于假设性证明，例如在格密码学中，学习错误（LWE）问题被认为是数学上困难的。LWE方案的安全性依赖于在高维网格中找到短向量的不可行性，即使在量子计算的情况下也是如此。严格的证明将加密方案的安全性与已研究的难题联系起来，表明任何对方案的有效攻击也将解决这些基础问题，这些问题被认为是抗量子的。

第三部分涉及实际实现，强调优化以提高程序速度并减少计算浪费。标准化是与NIST等组织合作制定商业规则的过程，确保程序遵循公认的准则。为了与当前技术兼容，后量子安全系统必须能够互操作。混合加密系统在过渡期间非常有用，因为它们允许旧系统继续使用并支持逐步采用。

第四部分介绍了现实世界测试，通过试点项目在受控环境中测试算法的实用性和发现问题。性能基准测试和安全审计是评估算法在现实环境中表现的重要手段。

第五部分讨论了过渡策略，强调混合系统在过渡初期的重要性，因为它们结合了经典和后量子方法以确保兼容性和安全性。过渡指南为组织提供了详细的步骤和最佳实践，以确保过渡过程的顺利进行。

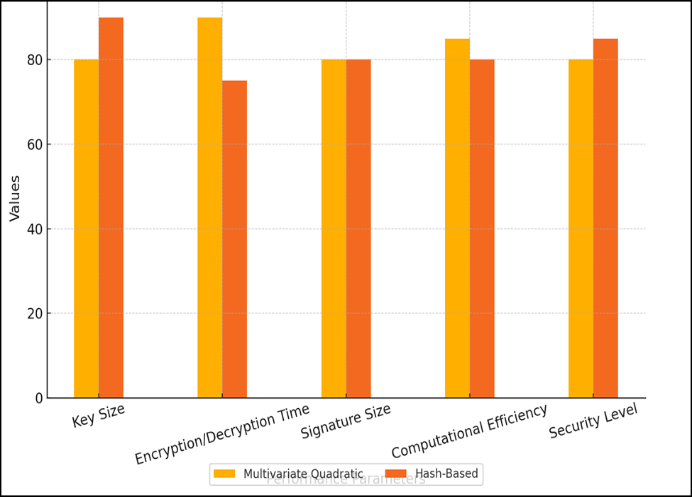
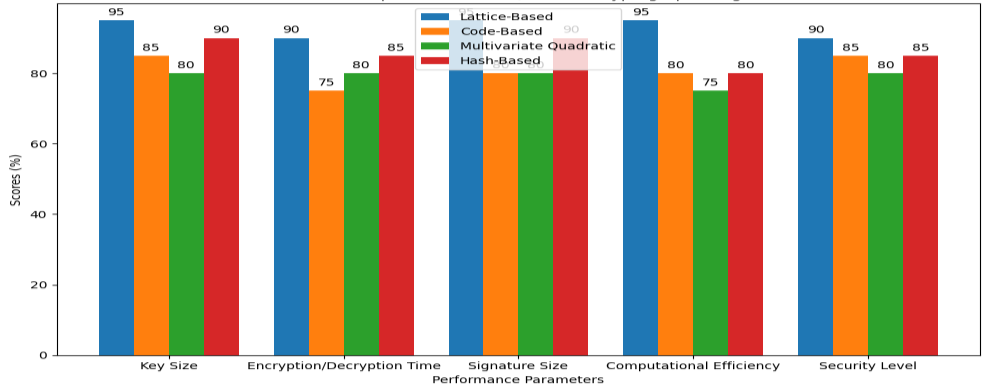
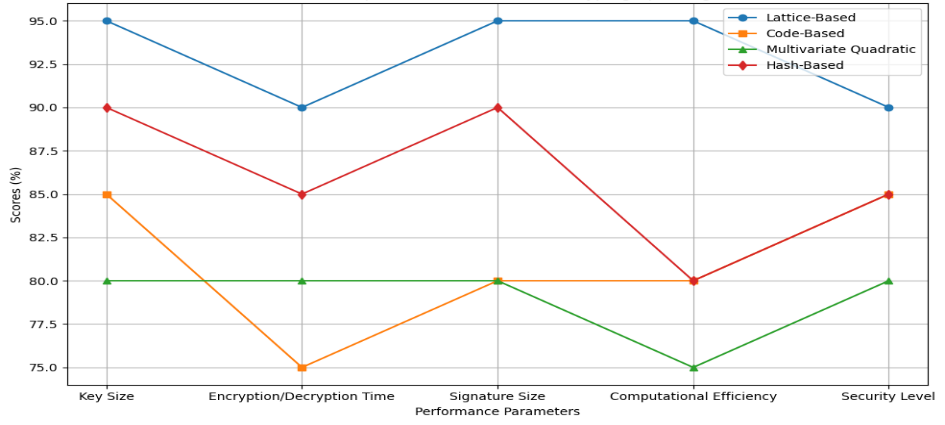
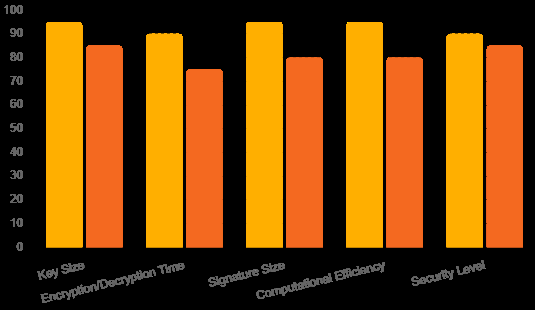
结果与讨论部分通过表格和图表比较了不同后量子密码算法的性能参数，如密钥大小、加密/解密时间、签名大小、计算效率和安全级别。格密码学在多个重要方面表现优异，是后量子标准的首选。代码密码学在密钥大小和安全级别方面表现良好，但其较大的密钥尺寸可能对某些用户不太方便。多变量二次方程在各方面表现尚可，是一种灵活的选择。基于哈希的密码学在易用性和提供良好安全性方面受到青睐。

结论部分指出，为了减轻量子计算可能带来的风险，必须开发和使用新的后量子加密方法。通过使用新的密码学方法、进行彻底的安全评估以及实施强有力的过渡计划，可以在量子时代及以后保持对加密系统的信任。

这篇论文通过详细探讨后量子密码学的各个方面，为在量子时代确保数据安全提供了全面的视角。它强调了开发新算法、分析其安全性、实际实现、现实世界测试以及过渡策略的重要性。通过这些研究，研究人员致力于开发基于数学难题的密码学方法，以抵御量子攻击。