使用张量重整化群方法的光谱学

该文档主要探讨了在(1+1)维Ising模型中使用张量网络方法进行谱学计算的研究。以下是对该文档的详细总结：

研究背景与动机

Ising模型是统计物理中研究相变和临界现象的经典模型。本文聚焦于**(1+1)维Ising模型**，即一个时间和一个空间维度的系统。传统上，计算这种模型的能谱需要处理庞大的转移矩阵，计算复杂度极高。为此，本文提出了一种基于张量网络的计算方法，旨在有效地估计转移矩阵的谱。

方法概述

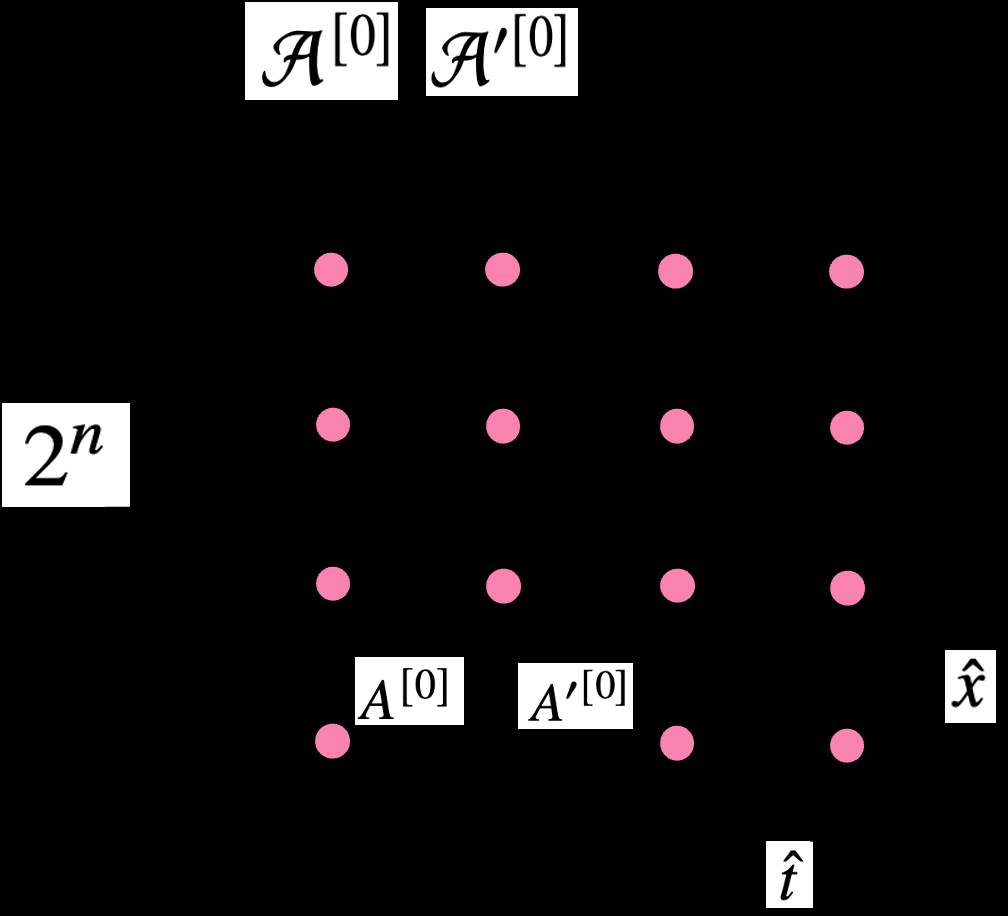
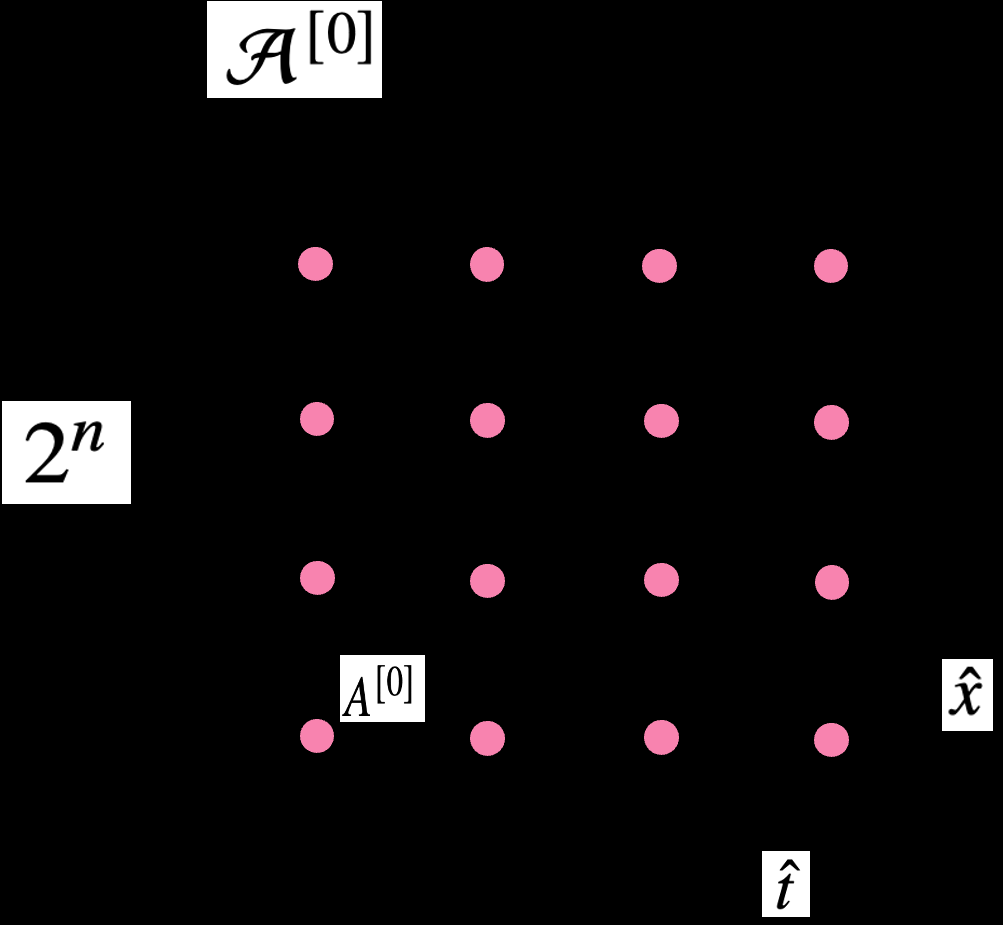
本文采用了高阶奇异值分解（HOTRG）方法来处理张量网络。HOTRG是一种粗粒化技术，能够在保持系统物理性质的同时，减少张量网络的维度。通过这种方法，研究者能够在较小的计算资源下，估计转移矩阵的谱。

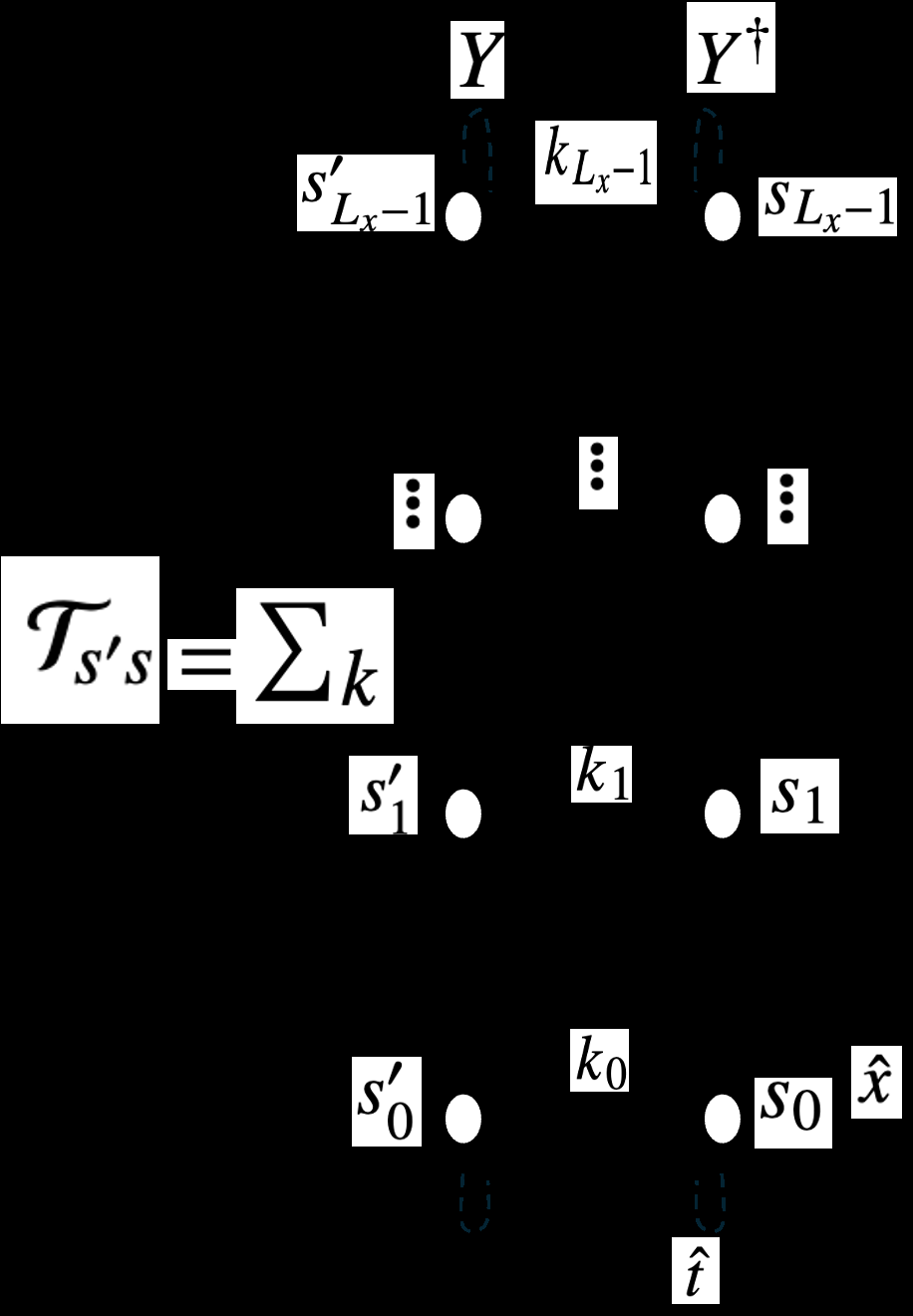
1. 转移矩阵与能谱计算：转移矩阵是描述系统状态随时间演化的核心工具。本文通过将分区函数表示为张量网络，利用HOTRG方法对其进行简化，从而估计转移矩阵的特征值（谱）。

2. 量子数分类：通过分析矩阵元素，研究者能够将能量本征态分为不同的量子数组。这种分类有助于理解系统的对称性和能级结构。

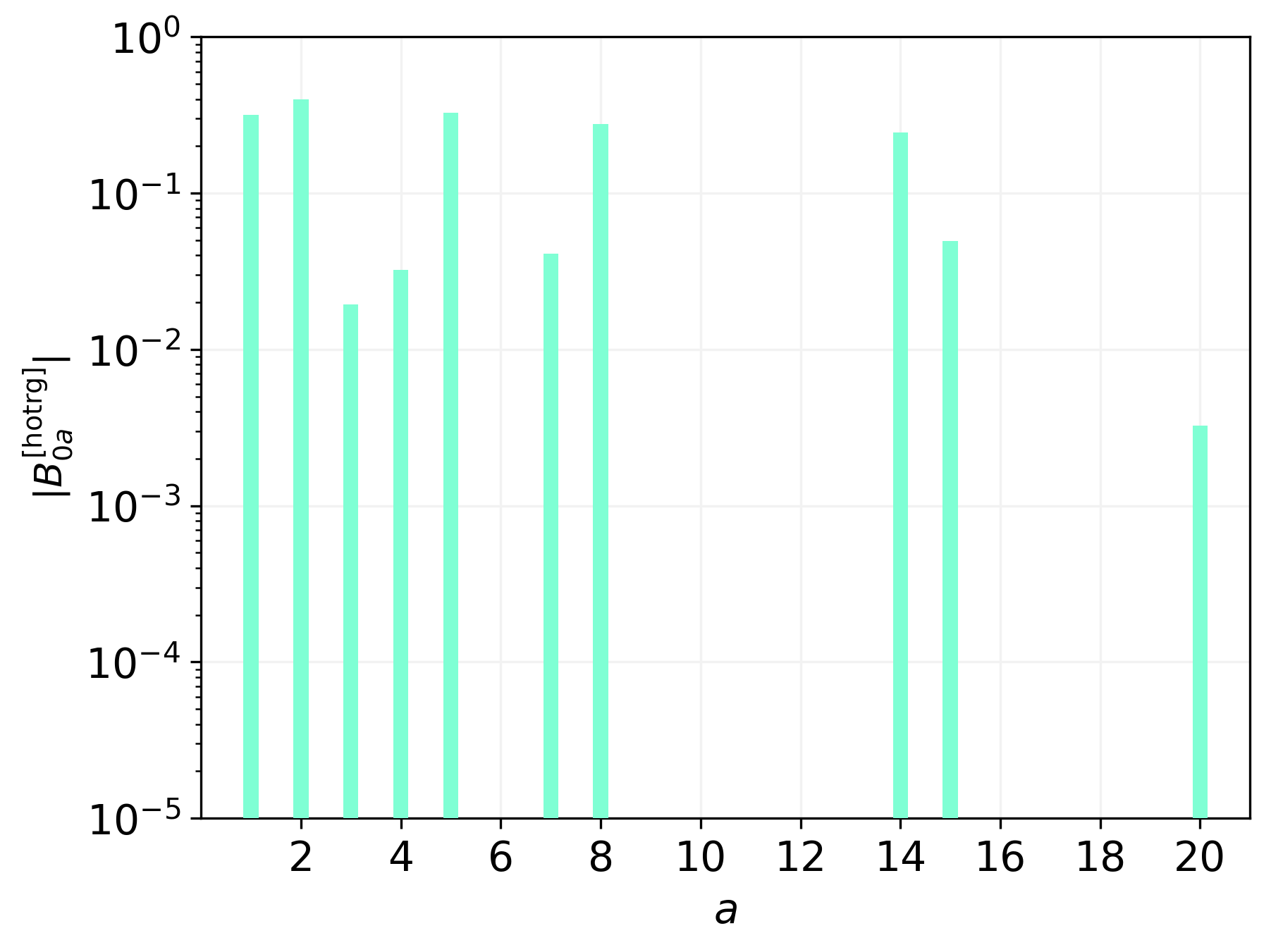
3. 动量识别：通过计算单自旋算符在动量空间的矩阵元素，研究者能够识别低激发态的动量。这对于理解系统的动力学行为至关重要。

主要结果

• 能量间隙计算：研究者在温度(T=2.44)和系统大小(L_x=64)的条件下，计算了前20个能量间隙。结果显示，能量本征态可以根据量子数(q={1, -1})进行分类。

• 相对误差分析：通过与精确能量间隙的比较，发现数值计算的相对误差在较高本征态时较大，最大误差在(O(10^{-2}))的量级。

• 散射相移：利用Lüscher公式，研究者计算了两粒子态的能量间隙和散射相移。数值结果与理论预期的相移(\delta_{\text{ising}}=-\pi/2)一致。

贡献与展望

本文提出了一种有效的谱学计算方案，结合转移矩阵和张量网络方法，成功应用于(1+1)维Ising模型。该方法不仅能够准确计算能量间隙和量子数，还能识别动量和计算散射相移。未来，研究者计划将该方法应用于(1+1)维标量场理论，并在运动框架中计算相移。

术语解释

• 张量网络：一种用于表示多体量子态的数学结构，通过节点和边表示张量及其相互作用。
• 高阶奇异值分解（HOTRG）：一种用于简化张量网络的技术，通过奇异值分解减少张量的维度。
• 转移矩阵：在统计物理中，用于描述系统状态随时间演化的矩阵。
• Lüscher公式：一种用于计算有限体积系统中散射相移的公式。

通过本文的研究，研究者展示了张量网络方法在处理复杂物理系统中的潜力，为进一步的理论和数值研究提供了新的工具和思路。