Kauffman模型中闭合性与开放式进化之间因果关系的证据

这篇论文探讨了生物进化的数学描述，特别是自组织和选择在达尔文进化中的作用。作者试图通过Kauffman模型来解释生物系统中功能性组织的出现与开放式进化（Open-Ended Evolution, OEE）之间的因果关系。

1. 研究动机

论文指出，理解生命系统的数学需要范式的根本性改变。现有的数学工具不足以准确预测生物体的动态，生物进化提出了一个极具挑战性的问题。作者的目标是找到描述进化的数学工具，提出“说出我们无法谈论的所有内容”的目标。

2. 关键概念

• 闭合性（Closure）：在生物系统中，某些量在特定时间尺度上是守恒的，被称为约束（constraints）。这些约束在不同时间尺度上会退化，需要被替换或修复。闭合性意味着一个约束集中的每个约束都依赖于另一个约束，并且至少有一个约束依赖于它。这种闭合性与生物系统的自主性、自我维持和自我生产能力相关。

• 变异原则（Principle of Variation）：生物系统被视为特定对象，其进化不仅依赖于对称性，还依赖于其历史和环境。生物系统的对称性会随着时间不可预测地变化，这种变化被称为开放式进化。

• 开放式进化与复杂性：Corominas-Murtra提出了开放式进化的三个公理，特别是第一个公理指出，开放式系统的复杂性不会随时间减少。复杂性的增加意味着系统中出现了新颖性，这种新颖性必须是功能性的，能够改变生物系统的组织。

3. 复杂性测量：装配（Assembly）

论文提出了一种新的复杂性测量方法，称为“装配”。装配量取决于两个主要参数：装配指数（assembly index）和复制数（copy number）。装配被解释为系统达到特定配置所需的“努力”的量度，也可以视为将系统带到特定配置所需的能量。

4. 假设与模型

作者假设功能闭合性和开放式进化之间存在强相关性，并认为闭合性是开放式进化的认识论原因。通过Kauffman模型，作者展示了自催化网络的出现如何影响装配的动态，并将自催化视为系统组织闭合的最简单表现。

5. 研究结果

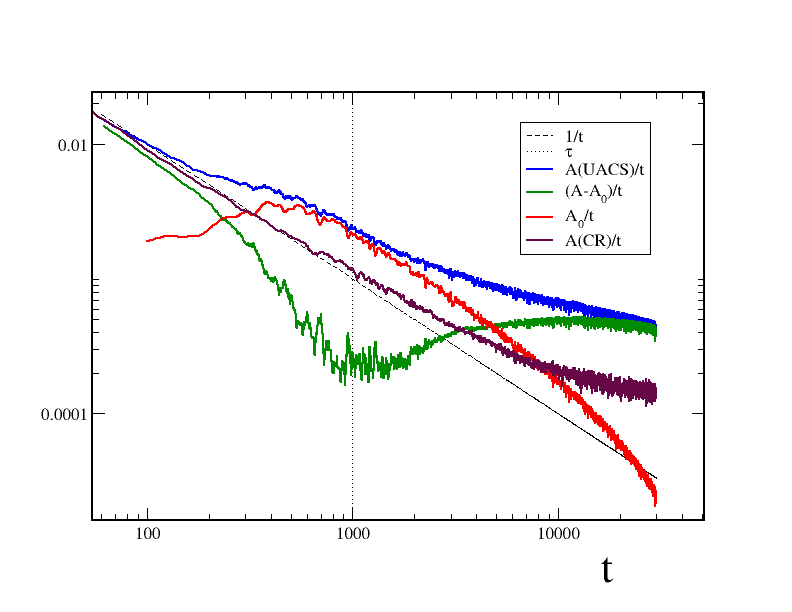
• 时间尺度的影响：研究表明，系统在不同时间尺度上的动态适应性，尤其是在自催化网络的影响下，复杂性会在长时间内达到一个稳定的水平。

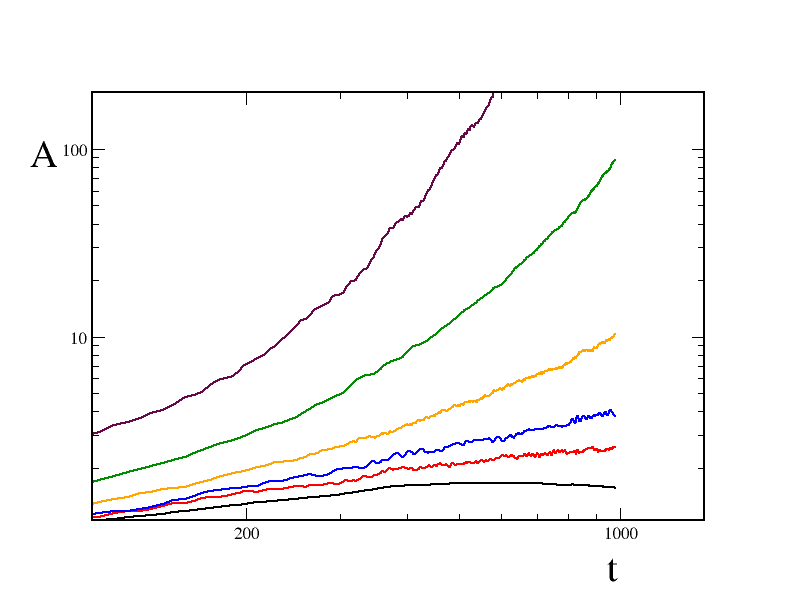
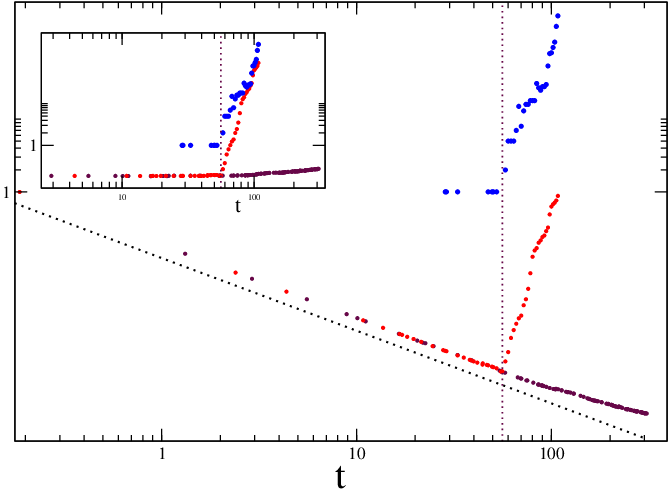
• 自催化网络的影响：自催化网络的出现对系统的复杂性有显著影响，尤其是在不同时间点引入自催化网络时，系统的反应显示出时间的普遍性。

6. 进一步发展

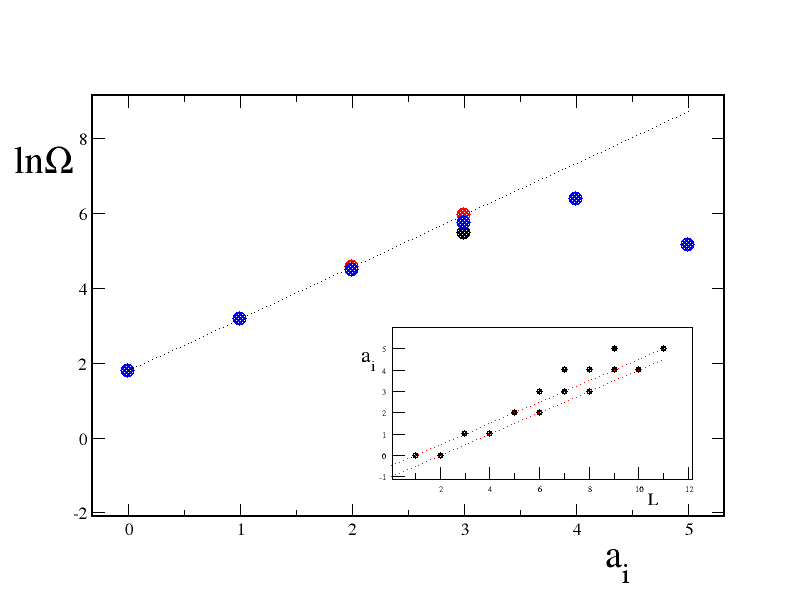
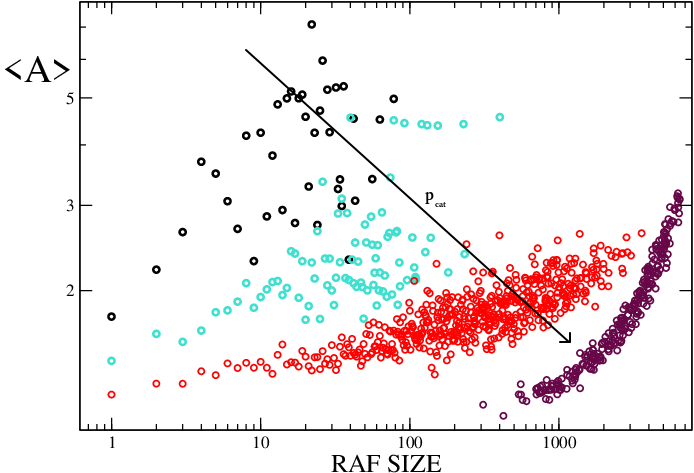
作者分析了自催化网络的出现对Kauffman模型中装配动态的影响，探讨了自催化循环的大小与装配之间的相关性，并展示了不同循环对装配的影响。

结论

论文通过数学模型和理论分析，提供了生物系统中功能性组织出现与开放式进化之间因果关系的证据。作者强调了选择和自组织在生物进化中的关键作用，并提出了新的复杂性测量方法，为理解生物进化提供了新的视角。

这篇论文为生物进化的数学描述提供了新的见解，特别是在理解生物系统的复杂性和开放式进化方面。通过引入装配作为复杂性的度量，作者为生物系统的数学建模提供了新的工具和方法。