多维非线性特征空间中支持向量机的量子计算加速研究

该文档主要探讨了**量子支持向量机（QSVM）**在多维非线性特征空间中的加速计算方法，并提出了一种结合经典计算和量子计算优势的新算法。以下是对该文档的详细总结：

1. 引言

支持向量机（SVM）是一种监督学习模型，广泛应用于模式识别、分类和回归分析。SVM通过解决二次规划问题来实现分类，但在处理大规模样本数据时，矩阵元素的数量随训练集规模的平方增长，导致计算复杂度高。**量子支持向量机（QSVM）**通过将SVM的二次规划问题转化为最小二乘问题，并利用量子算法高效解决关键步骤，如向量内积，从而显著降低计算复杂度。相比经典SVM，QSVM在处理大规模数据集时具有显著的计算效率优势。

2. 量子算法设计

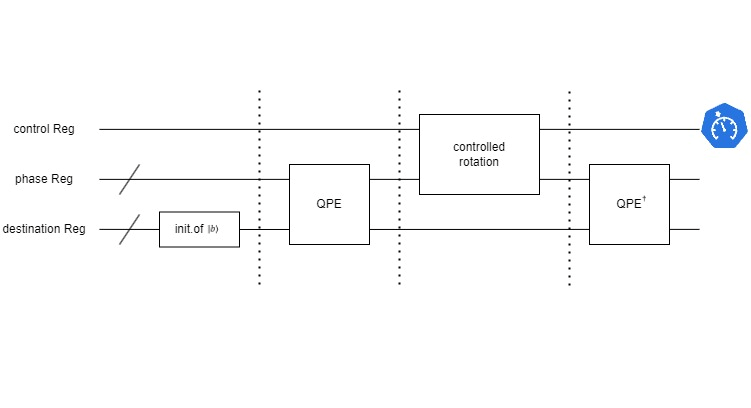
文中设计了一种结合经典和量子计算的计算架构，利用厄米矩阵的Pauli分解来模拟哈密顿量的量子模拟。基于HHL算法，设计了量子相位估计、量子傅里叶变换和量子态的条件旋转变换，以构建用于求解线性方程的量子电路，实现幺正算子的量子模拟。

• HHL算法：一种用于求解线性方程组的量子算法，能够在某些条件下实现指数级的加速。
• 量子相位估计：用于提取矩阵的特征值信息，是量子傅里叶变换的一个应用。
• 量子傅里叶变换：量子计算中的一种变换技术，用于将量子态从时域转换到频域。

3. 多维非线性特征空间处理

在处理多维非线性特征数据时，为避免高维空间中特征向量显式计算带来的高内存占用和计算复杂度，文中使用核方法将数据从原始空间映射到高维特征空间。核矩阵的每个元素表示高维空间中两个样本之间的内积。文中使用了线性核函数和径向基函数（RBF核）来处理线性和非线性数据。

• 核方法：一种通过计算核矩阵来避免显式构建高维特征空间的方法。
• 径向基函数（RBF核）：一种常用的核函数，用于处理非线性数据。

4. 支持向量机计算加速的实现

通过量子计算加速核矩阵的计算，并使用HHL算法显著加速线性系统的求解。相比经典解法，量子计算加速将复杂度从多项式级别降低到指数级别。首先通过核方法计算核矩阵，然后将矩阵和向量编码为量子态，通过量子相位估计获取矩阵的特征值信息，最终通过反向操作构建矩阵的逆。

5. 实验结果与分析

实验使用了Iris数据集，结果表明QSVM在分类性能、计算时间复杂度和内存需求方面优于经典SVM。特别是在处理高维和非线性特征时，QSVM表现出优越的分类能力。在计算时间和内存需求方面，QSVM显示出显著优势，尤其是在处理大规模数据集时。

6. 结论

文中研究了量子计算在多维非线性特征空间中对SVM的加速方法，并提出了一种结合经典和量子计算的新算法。实验结果显示，QSVM在分类性能、计算时间和内存需求方面优于经典SVM。然而，量子计算的实际应用仍面临诸多挑战，包括量子硬件的成熟度和量子误差的校正。未来的研究可以进一步探索更高效的量子映射算法和量子电路优化方法，以提高QSVM的性能和实用性。

通过以上总结，读者可以全面理解该文档的内容、方法和贡献。文中通过引入量子计算技术，显著提升了支持向量机在处理大规模、多维非线性数据时的效率，为SVM在大规模数据集中的应用提供了新的思路和方法。