阶段解锁：量子比特相位在量子计算中的关键作用

该文档是关于量子计算中量子比特（qubit）相位的重要性及其在量子算法中的作用的研究论文。以下是对该文档的详细总结：

引言

量子计算是一种利用量子力学原理进行计算的技术，旨在解决传统计算机无法处理的复杂问题。与经典计算机使用的比特不同，量子计算机使用量子比特（qubits），它们可以同时存在于多个状态（称为叠加态）。这种特性使得量子计算机在处理信息时具有更高的效率。此外，量子比特之间的纠缠现象进一步增强了计算能力。

量子比特相位的作用

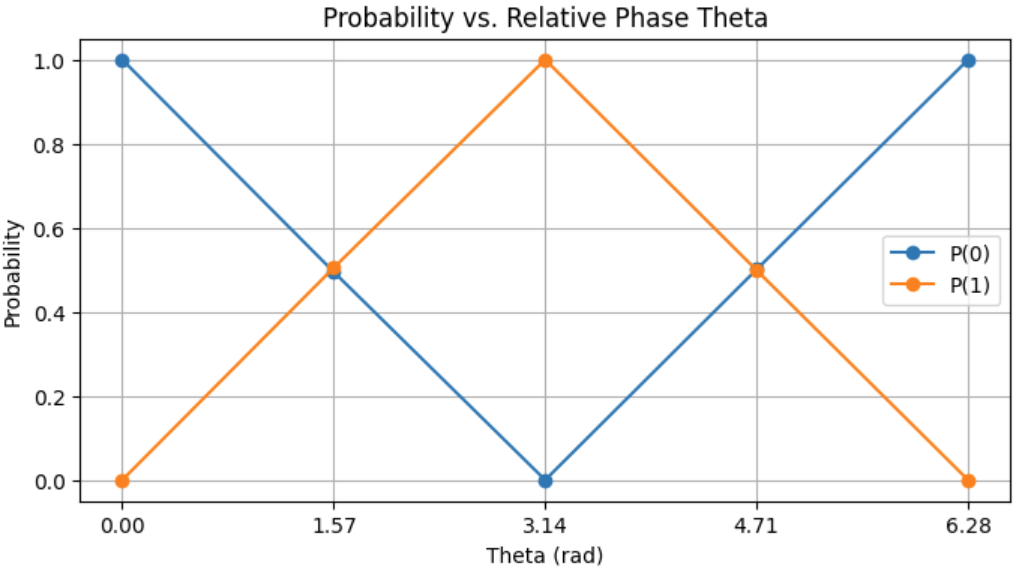
量子比特的状态不仅由幅度决定，还由相位变量定义。相位在量子计算中起着至关重要的作用，影响量子算法的效率和能力。论文探讨了相位如何通过相长干涉和相消干涉影响量子算法的基础。

• 相长干涉：当相位差导致概率幅度增加时发生。
• 相消干涉：当相位差导致概率幅度减少时发生。

量子门对相位的影响

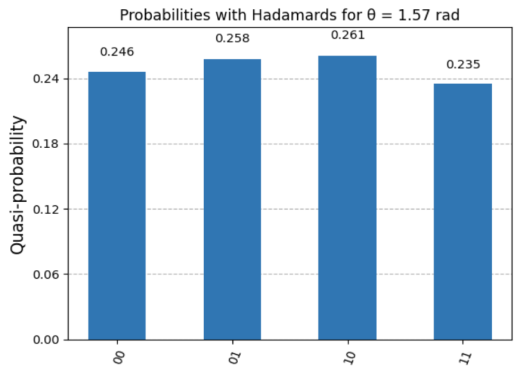
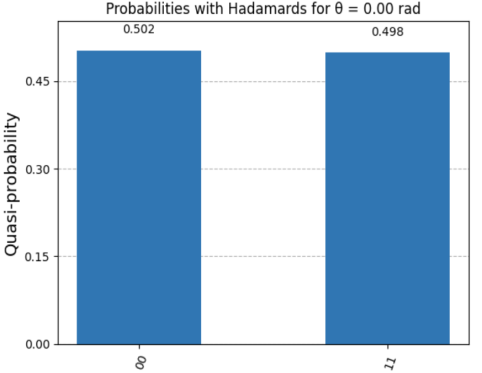
论文详细分析了常见的量子门（如Hadamard门、Pauli门和相位移门）如何改变量子比特的相位，从而影响其整体状态。通过使用Qiskit库的实际实现，展示了这些概念。

量子相位的数学框架

量子比特的状态可以表示为：
[ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle ]
其中，(\alpha)和(\beta)是复数幅度，满足归一化条件(|\alpha|^2 + |\beta|^2 = 1)。相位差在量子计算中至关重要，影响干涉模式和量子比特在变换下的演化。

全局相位与相对相位

论文强调了两种主要的相位类型：

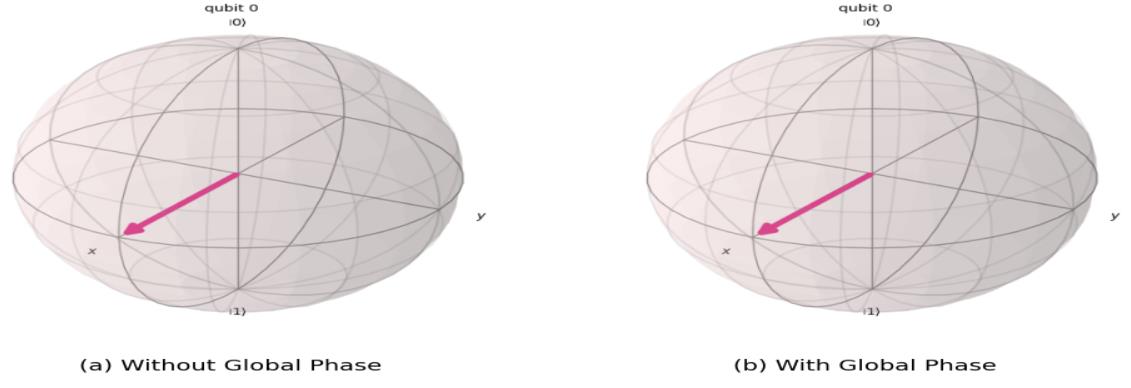
• 全局相位：不影响测量概率，但影响干涉。
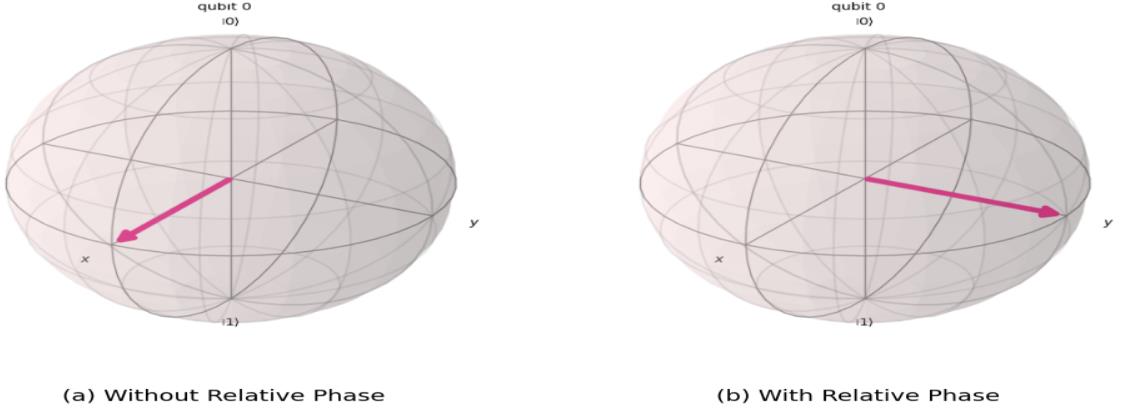
• 相对相位：叠加态分量之间的相位差，对于算法如Grover和Shor的算法至关重要。

相位操控的挑战

管理和监控量子比特相位具有内在的困难，特别是退相干的负面影响。退相干会破坏微妙的相位关系。论文描述了减轻这些障碍的策略，并探讨了间接提取相位信息的技术，如量子态层析和干涉测量。

量子算法中的相位应用

论文研究了相对相位在其他量子算法中的重要性，包括量子傅里叶变换（QFT）、量子相位估计（QPE）和Grover算法。这些算法利用相对相位的操控来生成干涉模式，从而放大期望的计算结果。

结论

论文总结了相位操控和理解对于量子计算发展的重要性。量子干涉是使量子算法优于经典算法的关键资源。对相位操控的掌握不仅有助于开发更高效的量子算法，还加深了对量子力学及其技术应用的理解。

贡献

该研究为量子计算中相位的关键作用提供了更深入的理解，为算法设计、量子控制和容错量子计算机的发展铺平了道路。

通过这篇论文，读者可以全面了解量子比特相位在量子计算中的重要性及其在量子算法中的应用，特别是在相位操控和干涉模式的生成方面的关键作用。