当冲击波在具有任意状态方程的流体中反射时的Richtmyer-Meshkov不稳定性

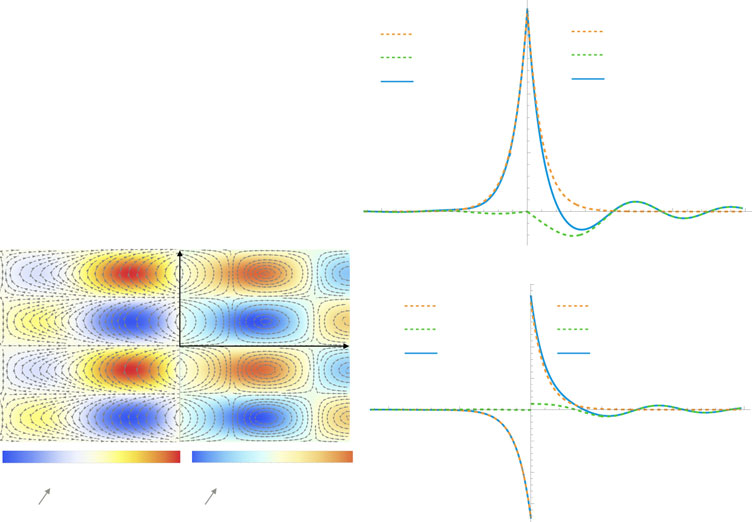
该文档主要探讨了瑞利-泰勒不稳定性（RMI）在反射冲击波情况下的线性分析，特别是涉及任意状态方程（EoS）的情形。本文的研究重点在于提供一种解析的、完全可压缩的理论，用于描述涉及反射冲击波的RMI问题。以下是对该文档的详细总结：

1. 研究背景与动机

瑞利-泰勒不稳定性（RMI）是流体动力学中的一个重要现象，通常发生在两种不同密度的流体界面受到加速时。本文特别关注反射冲击波的情形，这种情况下，冲击波在界面上反射并引发不稳定性。传统的研究方法通常依赖于特定的状态方程（EoS），而本文的一个重要贡献是不局限于任何特定的EoS，从而扩展了理论的适用范围。

2. 方法与理论框架

本文采用逆拉普拉斯变换（ILT）来解决初始值问题的扰动模型。与之前使用的变量分离技术不同，ILT方法能够在不同条件下提供更准确的解，尤其是在长时间尺度上。此外，本文还引入了双曲坐标变换来解析压力场，这种方法在附录中有详细描述。

• 状态方程（EoS）：描述流体的热力学状态，常见的有理想气体状态方程、范德瓦尔斯气体状态方程等。本文还考虑了三项本构方程用于简单金属的情况。
• 阿特伍德数（Atwood number, A0）：用于描述界面两侧流体密度差异的无量纲参数，定义为(A0 = \frac{\rho_{0t} - \rho_{0r}}{\rho_{0t} + \rho_{0r}})，其中(\rho_{0t})和(\rho_{0r})分别为界面两侧流体的密度。

3. 主要结果与发现

本文通过理论计算和数值模拟，得出了以下主要结论：

• 线性演化的精确模型：相比于启发式的预测模型，精确模型在冲击波不够弱的情况下具有更广泛的适用性。
• 不同EoS的比较：在比较现实的EoS与类似γ的EoS时，发现后者在某些情况下可能低估或高估界面波纹速度的增长率。
• 解析表达式的提供：本文提供了界面波纹速度的渐近增长率的显式表达式，并在多种条件下验证了其准确性。

4. 应用与意义

本文的研究不仅在理论上对RMI问题提供了更全面的理解，还在实际应用中具有重要意义。通过不局限于特定的EoS，本文的方法可以应用于更广泛的材料和条件下的RMI问题。此外，本文还提供了Mathematica代码，以便于其他研究人员进行进一步的研究和验证。

5. 结论

本文在RMI的线性研究中取得了重要进展，通过引入逆拉普拉斯变换和不依赖特定EoS的方法，提供了更为准确和广泛适用的理论框架。这一研究不仅丰富了RMI的理论基础，也为未来的实验和数值研究提供了有力的工具。

总之，本文通过创新的方法和广泛的适用性，为RMI的研究提供了新的视角和工具，具有重要的理论和实际意义。